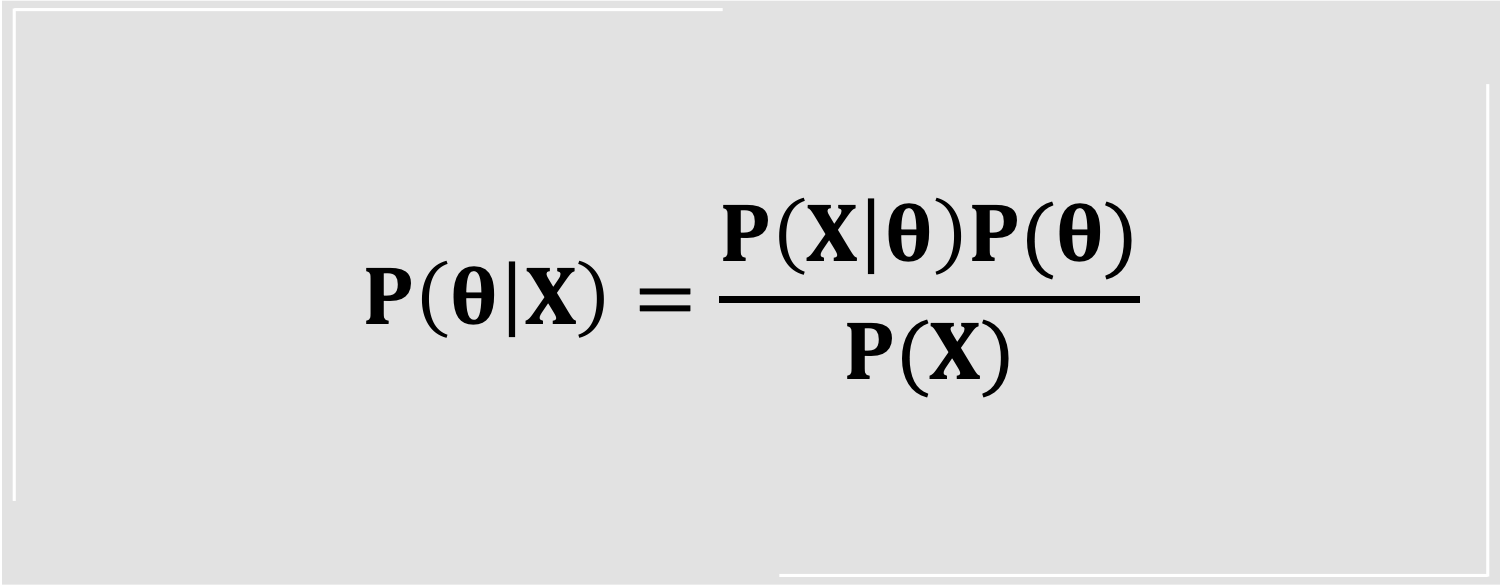
Temporal difference (TD) learning

TD($\lambda$) mechanism

TD(0) is one of TD learning method which considers only the next state, yet TD(1) is the other kind of TD learning which take the accumulated reward of the following states in the account. TD(1) is the well-known Monte-Carlo method. The difference between them is the target in evaluation function:

$$V(s) \gets V(s) + \alpha(\text{target} - V(s))$$

Furthermore, TD($\lambda$) is the generalized version contains both characteristic of TD(0) and TD(1), and is presented in the following example.

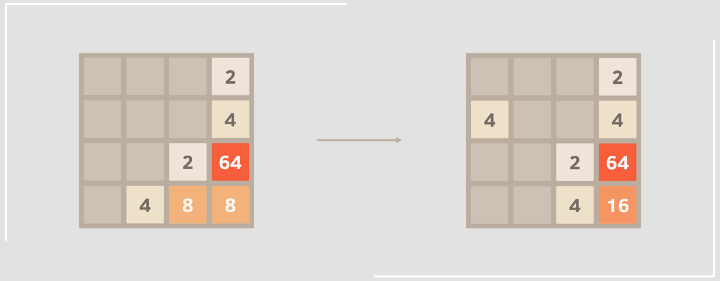
Here is one game composed only three actions:

$$s_0 - (a_0, r_0) - s_0’ \to s_1 - (a_1, r_1) - s_1’ \to s_2$$

The target($s_0$) of TD(0) and TD(1) is $r_0 + V(s_1)$ and $r_0 + r_1 + r_2$ respectively. For TD($\lambda$), the target is

$$\text{target}(s_0) = (1-\lambda) (r_1 + V(s_1)) + (\lambda \times (1-\lambda))(r_0 + r_1 + V(s_2)) + (\lambda \times \lambda) (r_0+r_1+r_2)$$

$$= r_0 + (1-\lambda)V(s_1) + \lambda \times \text{target}(s_1)$$

After-state

The after-state version uses the state after action to evaluate the value function.

$$s_0 - (a_0, r_0) - s_0’ \to s_1 - (a_1, r_1) - s_1’ \to s_2$$

$$V(s_0’) \gets V(s_0’) + \alpha(r_0 + V(s_1’) - V(s_0’))$$

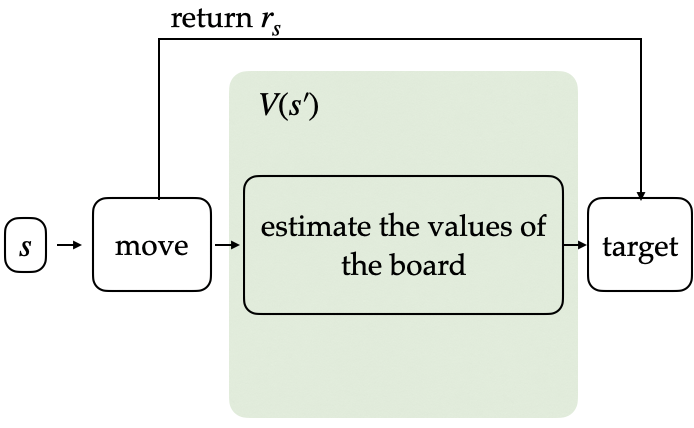
Decide the action based on the largest target.

Before-State

$$s_0 - (a_0, r_0) - s_0’ \to s_1 - (a_1, r_1) - s_1’ \to s_2$$

$$V(s_0) \gets V(s_0) + \alpha(r_0 + V(s_1) - V(s_0))$$

The (before-)state version uses the state before action to evaluate the value function.

Decide the action based on the largest target.

N-tuple network

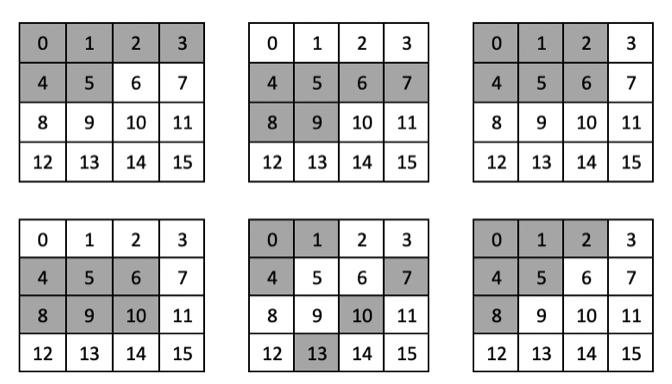
The goal of the n-tuple network is to use features to learn instead of the whole board. Each feature has 8 isomorphisms because of the rotation and reflection.

In my model, I train the model with 6 features that are shown below. The features are encoded as a 1-d array with length = $8 \times 16^6$  which is represented as $x(S)$. (All zeros, except 8 ones.) The value function is approximated by the linear combination of $x(S)$ and weight $\theta$. The elements of the vector   represent the scores of each tuple and are updated through the equation:

$$\theta \gets \theta + \alpha \Delta V\cdot x(S)$$

Practice

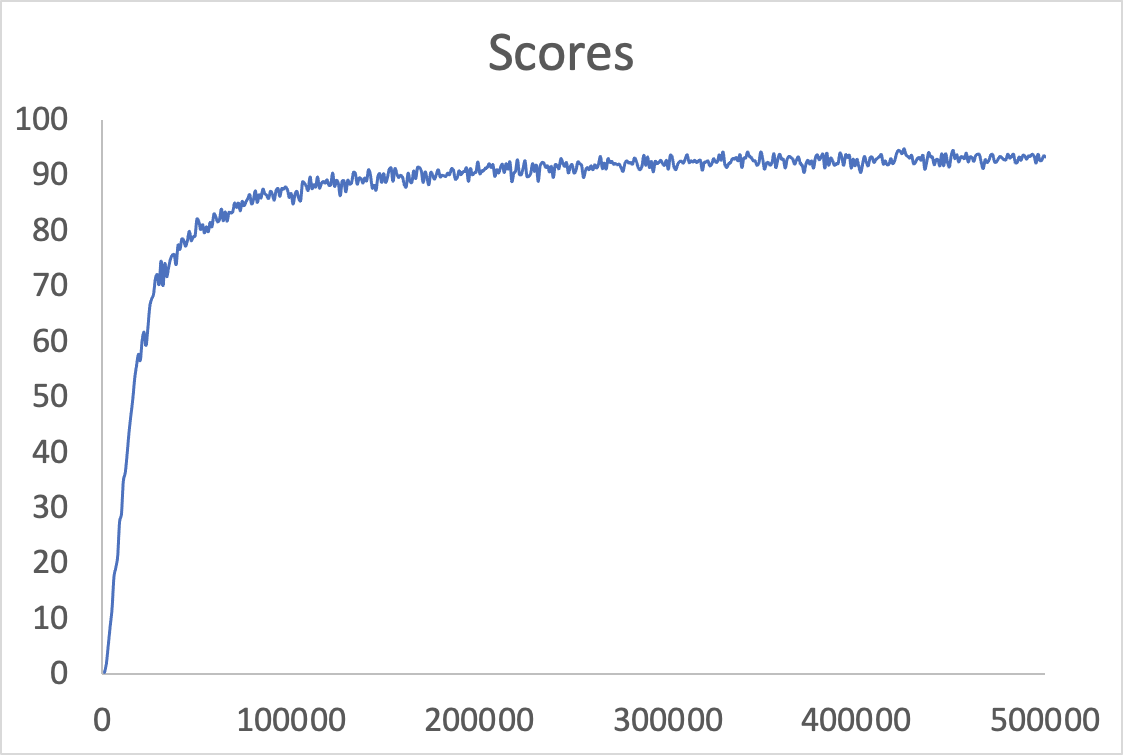
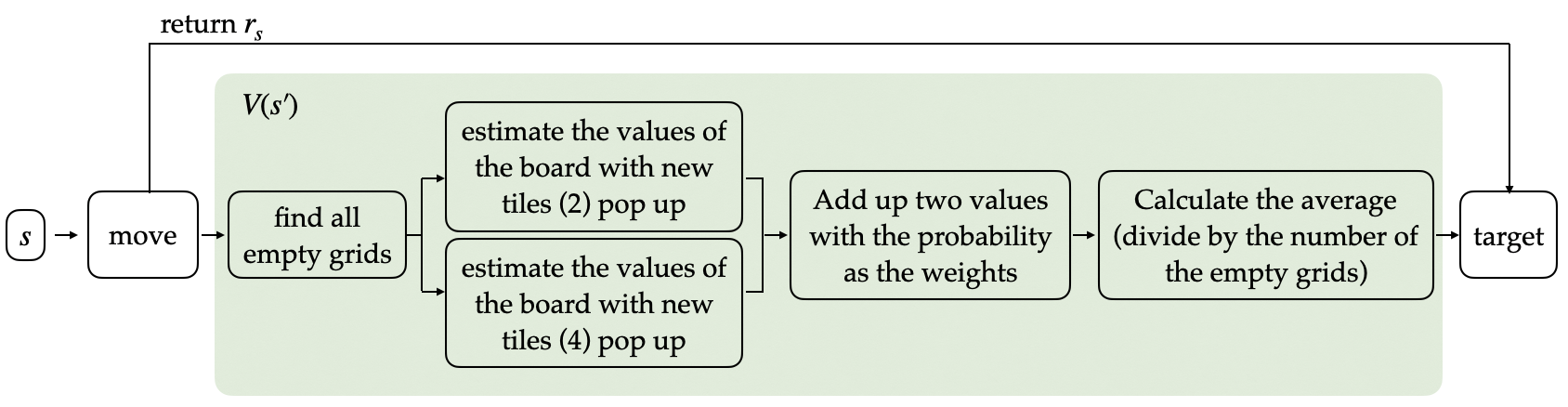
There are 5 functions assigned in the sample code. I revised 2 of them, “select_best_move” and “update_episode” and remain others the same with the demo code.

In “select_best_move” function, the key point is that the random tile pop-up with the probability needs to be considered in each move. Inspired by this concept, I add a for loop and an if statement to achieve.

In the loop, each grid will be check whether it is empty or not. In the empty grid, the 2-tile and 4-tile will be added and calculate theirs value (using “estimate” function), respectively. The values are summarised using weighted average with the weights 0.9 and 0.1. In the last, the value accumulated by the loop needs to divide by the number of the loop.

for (int i = 0; i < 16; i++) {
	if (after.at(i) == 0) {
		after.set(i, 1);
		value_ += 0.9 * estimate(after);
		after.set(i, 2);
		value_ += 0.1 * estimate(after);
		after.set(i, 0);
		zero_count ++;
	}
}
if (zero_count) value_ /= zero_count;

Second, the value updating through $V(s_t) \gets V(s_t) + \alpha(r_t + V(s_{t+1}) - V(s_t))$ is implemented in the “update_episode” function.

Compared to the demo code, 2 places are modified. One is that no initial expression in for statement since $V(s_{t+1})$ is adopted in updating $V(s_t)$. Using the example

to explain the steps in for loop:

float exact = 0;
for ( ; path.size(); path.pop_back()) {
	state& move = path.back();      
	exact += move.reward();
	float error = exact - estimate(move.before_state());
	exact = update(move.before_state(), alpha * error);
}

$$s_0 - (a_0, r_0) - s_0’ \to s_1 - (a_1, r_1) - s_1’ \to s_2$$

1. Select the final state $(s_2, s_2, x, -1)$.
2. Calculate target = $r_2 + V(s_{3})$ by **exact** = $(-1) + 0$.
3. Calculate $r_2 + V(s_{3}) - V(s_2)$ by **error** = exact - $V(s_2)$.
4. Update $V(s_2)$ by exact = $V(s_2) + \alpha (\text{error})$
5. Select the state $(s_1, s_1’, r_1, a_1)$.
6. Calculate target = $r_1 + V(s_{2})$ by **exact** = $r_1$ + exact
7. Calculate $r_1 + V(s_{2}) - V(s_1)$ by **error** = exact - $V(s_1)$
8. Update $V(s_1)$ by $V(s_1)+\alpha(\text{error})$
9. Repeat steps 5 to 8. (Replace $s_1$ by $s_0$ and $s_2$ by $s_1$).